1. W円の資産を持ち、ノイマン.モルゲンシュタインの期待効用定理の仮定を満たし、
危険回避的な消費者を考える。この消費者は、
(N)火災が起こらず、何の損害も発生しないか、
(A)将来自分の家が火災で消失し、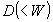 円の損害を被る 円の損害を被る
という、2つの状態からなるプロスペクトを持っているとする。また、この消費者は、
状態(A)が生じる確率は、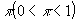 であると思っている。 であると思っている。
(1) 状態(N)が起こった時の資産額を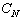 、状態(A)が起こった時の資産額を 、状態(A)が起こった時の資産額を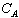 とする時、この消費者の無差別曲線は、 とする時、この消費者の無差別曲線は、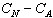 平面上でいかなる形を取るか?限界代替率はどのようになるか?
平面上でいかなる形を取るか?限界代替率はどのようになるか?
(2) 今、保険金1円について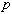 円(
円(
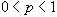 )の保険料を支払うことによって火災保険を購入できるとする。ただし、保険金 )の保険料を支払うことによって火災保険を購入できるとする。ただし、保険金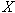 は は
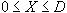 を満たさなければならない。この消費者の予算制約式(期末に実現可能な資産額の組の軌跡)を を満たさなければならない。この消費者の予算制約式(期末に実現可能な資産額の組の軌跡)を
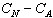 平面上に図示せよ。 平面上に図示せよ。
(3) 消費者の最適化問題を定式化し、最適解の満たすべき条件を述べなさい。
(4) 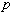 が下落した時に、消費者の保険購入のインセンティブ(
(3) の主体均衡)はいかに変化するか?比較静学を行なえ。図解と言葉での説明でよいが、その際、代替効果、所得効果の部分を明示すること。 が下落した時に、消費者の保険購入のインセンティブ(
(3) の主体均衡)はいかに変化するか?比較静学を行なえ。図解と言葉での説明でよいが、その際、代替効果、所得効果の部分を明示すること。
(5) 損害を完全にカヴァーするのはいかなる消費者か?
まったくカヴァーしないのは、いかなる消費者か?
解説
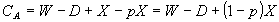
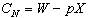 ただし、 ただし、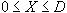
(1) 消費者が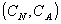 の組を選ぶときに得る期待効用は の組を選ぶときに得る期待効用は
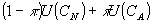
(2) 今、第2式で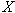 を消去して、 を消去して、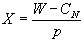 これを第1式に代入して、
これを第1式に代入して、
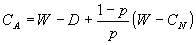 ――――① ――――①
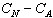 上に図示すると、 上に図示すると、
授業の図のようになる。
直感的に説明すれば、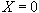 (保険を購入せず)を選ぶときの期末資産額の組は (保険を購入せず)を選ぶときの期末資産額の組は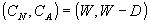 。この点から 。この点から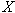 円だけ保険を購入すると、状態(N)が生起した時の期末資産額は 円だけ保険を購入すると、状態(N)が生起した時の期末資産額は
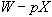 となり、保険料分 となり、保険料分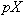 だけ減少するが、状態(A)が生起したときのそれは だけ減少するが、状態(A)が生起したときのそれは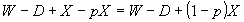 となり、保険金 となり、保険金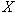 マイナス保険料 マイナス保険料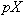 、すなわち 、すなわち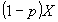 だけ増大する。予算制約線の傾き だけ増大する。予算制約線の傾き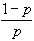 は、このトレードオフ は、このトレードオフ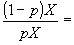 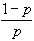 を表す。 を表す。
(3) この下で、彼の解く最適化問題は
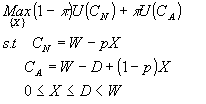
となる。制約条件の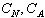 を目的関数に代入して を目的関数に代入して
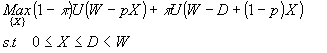
今、内点解を仮定すると、最適化の1階条件(First
Order Condition:F.O.C)は
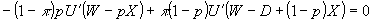 ―――② ―――②
この式の第1項は、1単位限界的に保険購入を増加させるとき、確率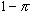 で状態Nが起り、その時は保険料 で状態Nが起り、その時は保険料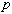 だけ損をする。これを効用タームに換算するために、期末資産額 だけ損をする。これを効用タームに換算するために、期末資産額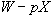 での限界効用 での限界効用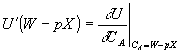 を掛ける。これらがトータルで状態Nでの期待限界不効用となる。第2項は、(1単位限界的に保険購入を増加させるとき、)確率 を掛ける。これらがトータルで状態Nでの期待限界不効用となる。第2項は、(1単位限界的に保険購入を増加させるとき、)確率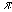 で状態Aが起り、その時はネットで保険金 で状態Aが起り、その時はネットで保険金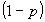 を受け取る。これを効用タームに換算すると、期末資産額 を受け取る。これを効用タームに換算すると、期末資産額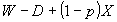 での限界効用
での限界効用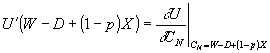 を掛けたものとなる。これらがトータルで状態Aでの期待限界効用となる。②はこれらがバランスするように保険金
を掛けたものとなる。これらがトータルで状態Aでの期待限界効用となる。②はこれらがバランスするように保険金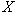 の額を決めるのが最適であることを述べている。 の額を決めるのが最適であることを述べている。
②を整理すると、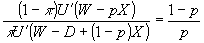 ――――③となる。左辺は限界代替率なので、これは、最適解において無差別曲線と予算制約線が接していることを示している。
――――③となる。左辺は限界代替率なので、これは、最適解において無差別曲線と予算制約線が接していることを示している。
補足
→
(5):端点解の条件とその意味付けへの参考。
この消費者が保険購入のインセンティブを持つためには、②の左辺を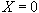 で評価して で評価して
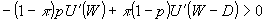 ―――④ ―――④
であれば良い。これは、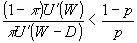 より、 より、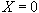 での限界代替率が、予算制約の傾き での限界代替率が、予算制約の傾き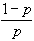 より小さいということに対応する。同様に全額保険をしない( より小さいということに対応する。同様に全額保険をしない(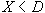 )ためには、 )ためには、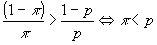 :「火災の生起(A)の見込み」が保険料よりも小さい必要がある。 :「火災の生起(A)の見込み」が保険料よりも小さい必要がある。
Back
|